Value at Risk e o Indicador ADX - Identificação de tendências

Este estudo foi feito por mim em 2015, utilizando o software estatístico R, mas para ilustrar a ideia do indicador ADX e falar sobre identificação de tendências e Value at Risk, ele ainda é bem atual. A parte o lado técnico e que indicadores sempre possuem atraso, vale a leitura do conceito para quem não é familiarizado com programação.

Hoje vamos aprender a calcular o VaR - Value at Risk - dos papéis e, utilizando o indicador técnico ADX, identificar quando um papel está ou não em tendência, seja de alta ou baixa.

Por definição, para entendimento rápido, o Value at Risk é uma medida do risco de perda dados os retornos observados de um ativo. Ele retornará, dada uma quantidade de investimento, a probabilidade de um certo montante perda ocorrer.

Já o indicador ADX, do inglês Average Directional Index, mede a força de uma tendência, independentemente de sua direção. Ele é acompanhado de mais outros dois indicadores, o +DI e o -DI que são os auxiliares para identificar a direção da tendência. De acordo com o mercado temos a seguinte tabela:

Valor do ADX  e  Força da Tendência

• 0 a 25 - Nenhuma ou fraca
• 25 a 50 - Forte
• 50 a 75 - Muito Forte
• 75 a 100 - Fortíssima

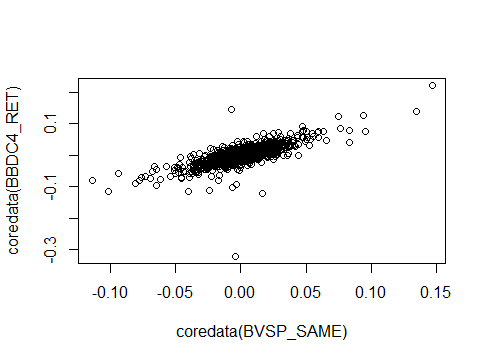
e se o indicador +DI é maior que o -DI, temos uma tendência de alta e vice-versa.

Na prática, vamos definir os parâmetros iniciais da nossa análise, com data de início em janeiro de 2008 e seleção do Índice Bovespa e das ações do Bradesco (BBDC4).

​library(Quantmod)   
 library(moments) # to get skew & kurtosis  
 #Seleção do período de análise  
 startDate = as.Date("2008-01-01")   
 endDate = as.Date("2014-12-19")  
 #Seleção das ações  
 tickers = c('^BVSP','BBDC4.SA')  
 #Captura dos dados  
 getSymbols(tickers, src = "yahoo", from = startDate, to = endDate)  
 #Cálculo dos retornos  
 BVSP_RET <- dailyReturn(BVSP)  
 BBDC4_RET <- dailyReturn(BBDC4.SA)  

Agora, vamos entender algumas função auxiliares necessárias para nosso código.

 #Funções auxiliares  
 index(BVSP_RET) #Retorna as datas (que estão como índice das linhas)  
 coredata(BVSP_RET) #Retorna os dados principais, ou seja, os valores  

Aqui vale uma observação: os dados retornados pela função getSymbols() não são um dataframe e sim um xts. Por isso, a index() retorna os índices de cada linha que, no caso, são os dias/datas das informações da ação. Sempre que selecionarmos alguma linha de um dado do tipo xts, ele sempre retornará uma informação com o índice o o corevalue. Assim, faz sentido a próxima função, coredata(). Ela nos retorna apenas os valores da ação (ou retorno, no caso), sem a informação de data acoplada. E por que gostaríamos de algo assim? Veremos logo adiante.

Vamos agora ajustar os dados do índice com os dados da ação BBDC4. Repare o comprimento de cada informação é diferente, ou seja, a getSymbols() não retornou exatamente as mesmas cotações para o Índice Bovespa e para as BBDC4 (problemas da fonte, que não precisamos debater agora).

 length(BVSP_RET) #1732  
 length(BBDC4_RET) #1662  

Temos 1732 registros de retornos para o BVSP e 1662 para BBDC4. Para alinhar as duas informações, vamos utilizar a função %in%.
​

length(BVSP_RET[index(BVSP_RET)%in%index(BBDC4_RET)]) #1662  

Com ela, retornamos todas as data (index) em comum entre BVSP_RET e BBDC4_RET, o que nos dá os 1.662 registros do BBDC4.

Podemos então plotar os retornos do IBovespa versus os retornos das BBDC4.

 ### Para plotar os mesmos dias dos retornos  
 #Atribui os valores que são conjuntos  
 BVSP_SAME <- BVSP_RET[index(BVSP_RET)%in%index(BBDC4_RET)]  
 plot(coredata(BVSP_SAME),coredata(BBDC4_RET))  

Aqui está a justificativa do uso da função coredata(). Ao executar o plot() apenas com BVSP_SAME e BBDC4_RET, teremos um erro de coordenadas, pois é como se estivéssemos passando 4 parâmetros para a função, ao invés de 2 (4 pois temos as informações de data para os dois ativos, assim como as informações dos retornos). Como resultado do nosso plot, temos:

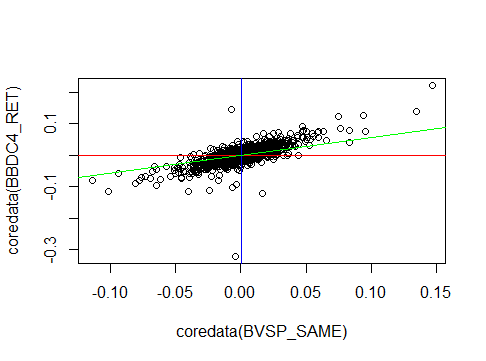
Apenas para fins didáticos, vamos plotar no mesmo gráfico a regressão dos retornos do Ibov em função dos retornos de BBDC4 e também plotar as medianas de retorno para cada ativo.

 fit_RET_BVSP_BBDC4 <- lm(BVSP_SAME~BBDC4_RET)  
 summary(fit_RET_BVSP_BBDC4)  
 abline(v=median(BVSP_SAME), col = "blue")  
 abline(h=median(BBDC4_RET), col = "red")  
 abline(fit_RET_BVSP_BBDC4, col="green")   

Como saída temos:

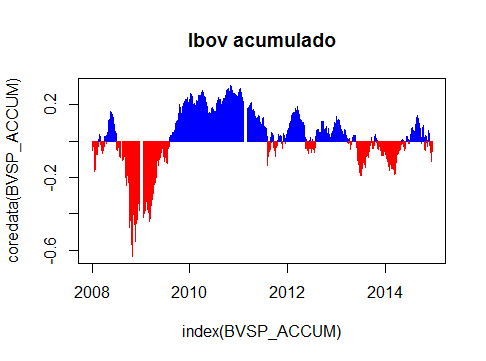
Agora, vamos calcular e plotar o retorno acumulado do Ibov e da BBDC4 com a função cumsum(). Também diferenciamos, através de um plot condicional, os períodos onde este retorno é posito ou negativo (azul e vermelho, respectivamente).

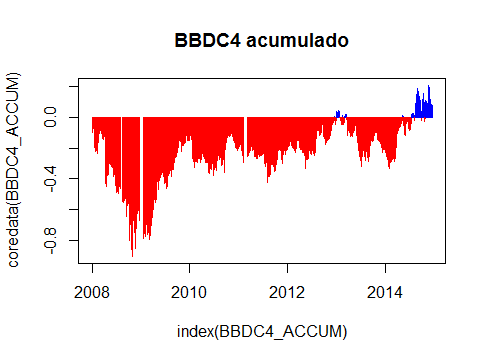
 #Retornos acumulados  
 BVSP_ACCUM <- cumsum(BVSP_SAME)  
 plot(index(BVSP_ACCUM),coredata(BVSP_ACCUM),  
    type = 'h',  
    col=ifelse(coredata(BVSP_ACCUM)>0,"blue", "red"),  
    main = "Ibov acumulado"  
    )  
 BBDC4_ACCUM <- cumsum(BBDC4_RET)  
 plot(index(BBDC4_ACCUM),coredata(BBDC4_ACCUM),  
    type = 'h',  
    col=ifelse(coredata(BBDC4_ACCUM)>0,"blue", "red"),  
    main = "BBDC4 acumulado"  
    )  

Graficamente,

Quem comprou BBDC4 ou investe de algum maneira proporcional ao Índice Bovespa, está no lucro, mesmo que marginal e abaixo do CDI.

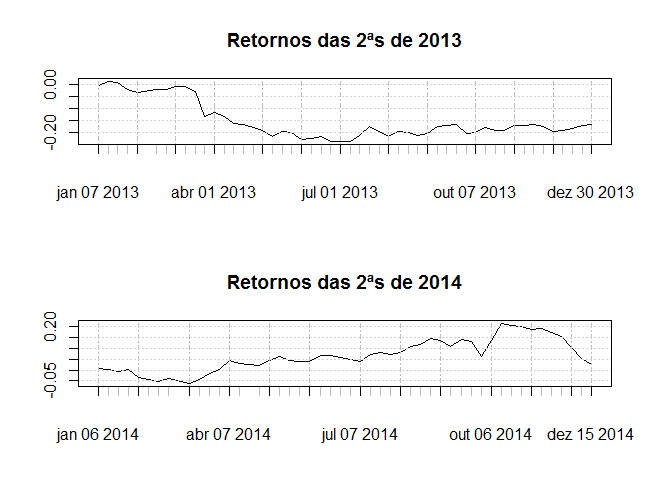
Voltando ao R, vamos particionar os dados de acordo com as informações anuais, já que temos data de início em 2008. Também vamos calcular os retornos por ano. O princípio utilizado aqui foi visto no post Subsetting no R.

 #Subseting dos retornos por ano  
 BBDC4_RET_2008 <- BBDC4_RET[index(BBDC4_RET)>'2008-01-01' & index(BBDC4_RET)<'2009-01-01']  
 BBDC4_RET_2009 <- BBDC4_RET[index(BBDC4_RET)>'2009-01-01' & index(BBDC4_RET)<'2010-01-01']  
 BBDC4_RET_2010 <- BBDC4_RET[index(BBDC4_RET)>'2010-01-01' & index(BBDC4_RET)<'2011-01-01']  
 BBDC4_RET_2011 <- BBDC4_RET[index(BBDC4_RET)>'2011-01-01' & index(BBDC4_RET)<'2012-01-01']  
 BBDC4_RET_2012 <- BBDC4_RET[index(BBDC4_RET)>'2012-01-01' & index(BBDC4_RET)<'2013-01-01']  
 BBDC4_RET_2013 <- BBDC4_RET[index(BBDC4_RET)>'2013-01-01' & index(BBDC4_RET)<'2014-01-01']  
 BBDC4_RET_2014 <- BBDC4_RET[index(BBDC4_RET)>'2014-01-01' & index(BBDC4_RET)<'2014-12-19']
  
 #Calculo dos retornos acumulado por ano  
 BBDC4_ACCUM_2008 <- cumsum(BBDC4_RET_2008)  
 BBDC4_ACCUM_2009 <- cumsum(BBDC4_RET_2009)  
 BBDC4_ACCUM_2010 <- cumsum(BBDC4_RET_2010)  
 BBDC4_ACCUM_2011 <- cumsum(BBDC4_RET_2011)  
 BBDC4_ACCUM_2012 <- cumsum(BBDC4_RET_2012)  
 BBDC4_ACCUM_2013 <- cumsum(BBDC4_RET_2013)  
 BBDC4_ACCUM_2014 <- cumsum(BBDC4_RET_2014)  

Com estes dados particionados, podemos utilizar algumas funcionalidades do R para fazer uma análise exploratória dos retornos. Utilizamos a função weekdays() para recuperar as informações de qual é o dia da semana correspondente à data no index(). Em seguida, calculamos apenas os retornos acumulados das segundas-feiras de 2013 e 2014.

 #Retorna os dias da semana dos retornos  
 weekdays(index(BBDC4_RET_2014))  
 #Retornos das segundas-feiras de 2013  
 BBDC4_SEG_2013 <- BBDC4_RET_2013[weekdays(index(BBDC4_RET_2013)) == "segunda-feira"]  
 #Retornos das segundas-feiras de 2014  
 BBDC4_SEG_2014 <- BBDC4_RET_2014[weekdays(index(BBDC4_RET_2014)) == "segunda-feira"]  

Graficamente, temos:

Não que tenha algum sentido lógico, mas estamos apenas demonstrando a capacidade de segmentação dos dados. Só por curiosidade, investindo apenas nas segundas-feiras em 2013, você teria tido um retorno máximo de apenas 1,18%. Já em 2014, teria alcançado 21,75%. Estes dados foram extraídos com a função max() aplicada na cumsum() que explicamos acima. Poderíamos ainda utilizar o comando table() para identificar quantas segundas tiveram retorno positivo ou negativo.

Vamos continuar agora calculando os percentis de 5% e 95% para o Bradesco, em 2014.

 #Retonar percentis de 5% e 95%  
 quantile(BBDC4_RET_2014,probs=c(0.05,0.95))  
         5%         95% 
-0.03516820  0.03867403 

Ou seja, 5% dos retornos de BBDC4 são menores que -3,51% e 95% dos retornos são menores que 3,87%. Agora, utilizando a mesma função quantile(), vamos ao cálculo do Value at Risk do Bradesco e do IBovespa para 2014.

 #VaR BBDC4 e BVSP  
 BVSP_RET_2014 <- BVSP_RET[index(BVSP_RET)>'2014-01-01' & index(BVSP_RET)<'2014-12-19']  
 Investimento <- 10000  
 quantile(BBDC4_RET_2014,probs=c(0.01,0.05))  
 BBDC4_VaR_2014 <- Investimento * quantile(BBDC4_RET_2014,probs=c(0.01,0.05))  
 BBDC4_VaR_2014
      1%       5% 
-570.021 -351.682   
 quantile(BVSP_RET_2014,probs=c(0.01,0.05))  
 BVSP_VaR_2014 <- Investimento * quantile(BVSP_RET_2014,probs=c(0.01,0.05))  
 BVSP_VaR_2014  
       1%        5% 
-361.3566 -247.9905 

Baseada na distribuição dos retornos diários, R$10.000 investidos na BBDC4 resultariam numa perda de R$570,02 ou mais com 1% de probabilidade ou R$351,68 ou mais com 5% de probabilidade. Os mesmos valores para o IBovespa são R$361,36 e R$247,99. Ou seja, é mais arriscado investir em BBDC4 do que no índice como um todo. Até soa razoável, já que o índice é uma ponderação de vários papéis sujeito a risco sistêmico e não apenas setorial.

Fechando a nossa análise, temos agora o cálculo do ADX para identificar tendências e suas intensidades, desde 2008.

 #Identificação de tendência com ADX  
 valorADX <- ADX(BBDC4.SA,n = 11, maType="EMA")  
 WEAK_HIGH_TREND <- ifelse(valorADX$ADX > 0 & valorADX$ADX <= 25 & valorADX$DIp > valorADX$DIn,1,0)  
 STRONG_HIGH_TREND <- ifelse(valorADX$ADX > 25 & valorADX$ADX <= 50 & valorADX$DIp > valorADX$DIn,1,0)  
 VERY_STRONG_HIGH_TREND <- ifelse(valorADX$ADX > 50 & valorADX$ADX <= 75 & valorADX$DIp > valorADX$DIn,1,0)  
 EXTREMILY_STRONG_HIGH_TREND <- ifelse(valorADX$ADX > 75 & valorADX$DIp > valorADX$DIn,1,0)  
 WEAK_LOW_TREND <- ifelse(valorADX$ADX > 0 & valorADX$ADX <= 25 & valorADX$DIn > valorADX$DIp,1,0)  
 STRONG_LOW_TREND <- ifelse(valorADX$ADX > 25 & valorADX$ADX <= 50 & valorADX$DIn > valorADX$DIp,1,0)  
 VERY_STRONG_LOW_TREND <- ifelse(valorADX$ADX > 50 & valorADX$ADX <= 75 & valorADX$DIn > valorADX$DIp,1,0)  
 EXTREMILY_STRONG_LOW_TREND <- ifelse(valorADX$ADX > 75 & valorADX$DIn > valorADX$DIp,1,0)  

Utilizamos a função ADX(), com uma média móvel exponencial (EMA) de 11 períodos (n=11). A lógica dentro das variáveis está baseada na tabela do começo do post e no fato do indicador +DI (DIp no R) ser maior que o -DI (DIn) para uma tendência de alta e o contrário para uma tendência de baixa. Com o comando table(), vamos entender por quanto tempo as ações do BBDC4 ficaram em uma tendência forte de alta (STRONG_HIGH_TREND).

 table(STRONG_HIGH_TREND)/sum(table(STRONG_HIGH_TREND))
STRONG_HIGH_TREND
        0         1 
0.7262265 0.2737735   

Apresentamos o cálculo já em percentual. Neste caso, desde 2008, as ações do BBDC4 estiveram 27,37% dos pregões em uma tendência forte de alta, segundo o indicador ADX. Apenas por curiosidade, foram 12% dos pregões em uma tendência forte de baixa. Use o código completo disponível no GitHub do Arte dos Dados, no repositório Computational Finance, para fazer suas próprias manipulações. O arquivo é o VaR_ADX_BBDC4_BVSP.R

Um abraço e até o próximo post!
​