|
Auto correlação, auto cointegração, modelos auto regressivos. Neste vídeo trago uma introdução para qualquer nível de conhecimento, com aplicação prática de um tema fascinante nas finanças quantitativas.
Download da planilha
0 Comments
A simulação de Monte Carlo é uma das áreas de estudo da probabilidade que se baseia em simular inúmeras possíveis saídas de um evento para facilitar a tomada de decisão.
Estas simulações são usadas para modelar a probabilidade de resultados diferentes em um processo que não pode ser facilmente previsto devido à intervenção de variáveis aleatórias. É uma técnica usada para entender o impacto do risco e da incerteza nos modelos financeiros. Leandro Guerra - Outspoken Market¶http://www.outspokenmarket.com Ibovespa - Análise de risco com Monte Carlo¶Quer entender mais sobre a teoria? Assista aqui¶
Todas as análises produzidas aqui foram feitas com a linguagem R e dados extraídos do Yahoo Finance
In [1]:
# Importando as bibliotecas
library(quantmod)
library(tidyverse)
options(warn=-1)
Vou selecionar os dados do Índice Bovespa do último triênio: 2017 à 2019
In [2]:
tickers <- c("^BVSP")
# Período
startdate <- as.Date("2015-01-01")
enddate <- as.Date("2019-12-31")
getSymbols(tickers, src = "yahoo", from = startdate, to = enddate)
BVSP <- data.frame(BVSP, stringsAsFactors = FALSE)
BVSP$Data <- as.Date(as.character(rownames(BVSP)))
names(BVSP) <- c("Abertura", "Maxima", "Minima", "Fechamento", "Volume", "Ajuste", "Data")
Agora, calculo o rertono para cada dia de pregão
In [3]:
# Calculando os retornos e o alvo
BVSP <- mutate(BVSP, Fechamento_lag = lag(Fechamento)) # vai criar um NA na primeira linha
BVSP <- na.omit(BVSP)
BVSP$Retornos <- (BVSP$Fechamento/BVSP$Fechamento_lag-1)
BVSP <- BVSP %>% select(Data, everything())
head(BVSP)
Como o mercado se comportou nestes últimos 3 anos?
In [5]:
par(mfrow=c(2,1))
plot(BVSP$Data, BVSP$Fechamento, type = "l", col = "blue", lwd = 2,
main = "Fechamento do Ibovespa em 2015-2019",
xlab = "2015 - 2019",
ylab = "Fechamento")
plot(BVSP$Data, BVSP$Retornos*100, type = "l", col = "black", lwd = 2,
main = "Retornos Diários do Ibovespa em 2015-2019",
xlab = "2015 - 2019",
ylab = "Retorno em %")
 Análise de risco com Monte Carlo¶Nesta etapa, vou calcular os parâmetros de entrada para a simulação de Monte Carlo
In [6]:
#Parametros do processo
#Retorno anual (Média de 2015/2019)
u <- ((last(BVSP$Fechamento)/first(BVSP$Fechamento))-1)/5
#Desvio padrão anual hipotético - 10%
sd <- 0.1
# Parâmetro de tempo
periodo <- 1:256
anos <- 5
A próxima etapa apresenta o cálculo dos valores simulados, totalizando 100,000 simulações
In [7]:
# Simulações
n_sim <- 100000
total_sim <- matrix(0, nrow = 256, ncol = n_sim)
p_inicial <- last(BVSP$Fechamento)
for(j in 1:n_sim){
aux <- 2
p <- p_inicial # Preço inicial
preco <- c(p) # Vetor para acumular os precos ao longo do tempo
dist <- rnorm(255,0,1) # Distribuição normal, 255 valores, com média 0 e desvio p. 1
for(i in dist)
{
P = p + p*(u/255 + sd/sqrt(255)*i)
preco[aux] <- P
p = P
aux = aux + 1
}
total_sim[,j] <- preco
}
Visualização das Simulações¶
In [8]:
matplot(total_sim
, main = "Ibovespa - Monte Carlo - Outspoken Market"
, xlab = "Tempo"
, ylab = "Preço"
, type = "l"
, col = 1:n_sim)
 Qual é chance de termos preços em zonas específicas?
In [9]:
round(quantile(total_sim, probs = c(0.05,0.95)), 2)
Disto, tem-se que 5% dos preços simulados são menores que 115,534.17 pontos e 95% estão abaixo de 162,644.37 E qual é o valor mínimo das 100,000 simulações?
In [10]:
round(min(total_sim),2)
Calculando o Value at Risk - VaR
In [11]:
round((1-p_inicial/quantile(total_sim, probs = c(0.01, 0.05)))*100, 2)
Estes resultados indicam uma perda (dia) de -3.27% ou mais com 1% de probabilidade ou -0.37% ou mais com 5% de probabilidade
Quando investidores e traders ouvem o termo "evento binário", geralmente pensam em empresas de biotecnologia que explodem de preço com a aprovação do FDA ou em uma empresa que teve suas ações desvalorizadas pela metade (ou pior) devido a má administração.
A Axsome Therapeutics (AXSM), cujas ações saltaram de US $ 45 / ação para mais de US $ 80 / ação em meados de dezembro é um bom exemplo do primeiro, enquanto o Bear Stearns e o Lehman Brothers, que efetivamente faliram durante a crise financeira de 2008, estão grandes exemplos deste último. No mercado, acontecimentos dramáticos que desencadeiam grandes movimentos são freqüentemente chamados de "eventos binários". Em retrospectiva, essas ocorrências podem ser facilmente interpretadas como positivos absolutos ou negativos absolutos, por meio de movimentos irregulares no histórico de preços. Índices de ações como o S&P 500, o Nasdaq e o Dow são teoricamente menos suscetíveis a movimentos binários extremos, porque compreendem um grande número de empresas diversificadas. As ações individuais, por outro lado, são mais suscetíveis a movimentos binários porque, com essas entidades, não há lugar onde se esconder - essas ações são compradas ou vendidas em imensos volumes, de acordo com o sentimento predominante após um evento crítico. O exposto acima ajuda a explicar por que a definição de um "evento binário" é um pouco diferente para os índices de ações em comparação com as ações individuais e também por que o risco (ou seja, o prêmio da opção e a volatilidade implícita) tem um preço tão diferente para cada uma. Uma correção para 2020?
O Dow Jones moveu-se apenas três vezes mais de 10% em uma única sessão (preço de abertura ao preço de fechamento, mesmo dia de negociação), incluindo:
Uma “correção” de mercado é frequentemente definida como uma retração de pelo menos 10% (alguns dizem mesmo 20%), o que significa que, em 1929 e 1987, os mercados foram corrigidos em um único dia. Ao considerar que a história do Dow abrange mais de 120 anos de negociação, o fato deste ter caído mais de 10% apenas três vezes é um testemunho da raridade de tais ocorrências. Olhando para a história mais recente (nos últimos 30 anos), houve zero casos em que o Dow Jones caiu pelo menos 10% em um único pregão. No entanto, houveram dois períodos nesse intervalo de tempo em que as bolsas de valores sofreram sérias correções. É claro que isso inclui 2000-2002 (a bolha pontocom) e 2008-2009 (a crise financeira).
Durante essas duas correções, houveram quatro dias de negociação em que o Dow Jones movimentou mais de 7% em um único dia (17 de setembro de 2001, 9 de outubro de 2008, 15 de outubro de 2008 e 1 de dezembro de 2008) .
O exposto acima ajuda a explicar por que os participantes do mercado ficam especialmente sensíveis ao movimento descendente destes durante o outono, porque cada um dos sete maiores movimentos de queda em um dia do Dow ocorreu em setembro ou outubro. O fato de a bolha pontocom e a crise financeira de 2008 terem apenas quatro dias no total em que o Dow Jones caiu mais de 7% é mais uma evidência de que esses movimentos são extremamente raros. Avançando rapidamente para os dias atuais, o mercado de ações dos EUA está em alta desde a última correção séria em 2008-2009. Durante esse período, o S&P 500 atingiu o fundo do poço em torno de 676. Recentemente, o S&P 500 fechou perto de 3.250, representando um aumento de mais de 380% em pouco menos de 11 anos. Embora os detentores de ações de longo prazo devam estar satisfeitos com 2019, é preciso pensar que há um bom número de traders contrários por aí afiando suas facas em antecipação à próxima grande correção do mercado. Em algum momento no futuro, a atual alta do mercado será refletida como uma corrida de touros impressionante que teve um ponto de partida e um ponto de chegada bem definidos. É quase garantido que o futuro "ponto final" do atual mercado em alta catalisará uma nova rodada de livros e filmes na mesma linha que The Big Short. Então, quais são as chances de que ocorra um recuo em 2020?
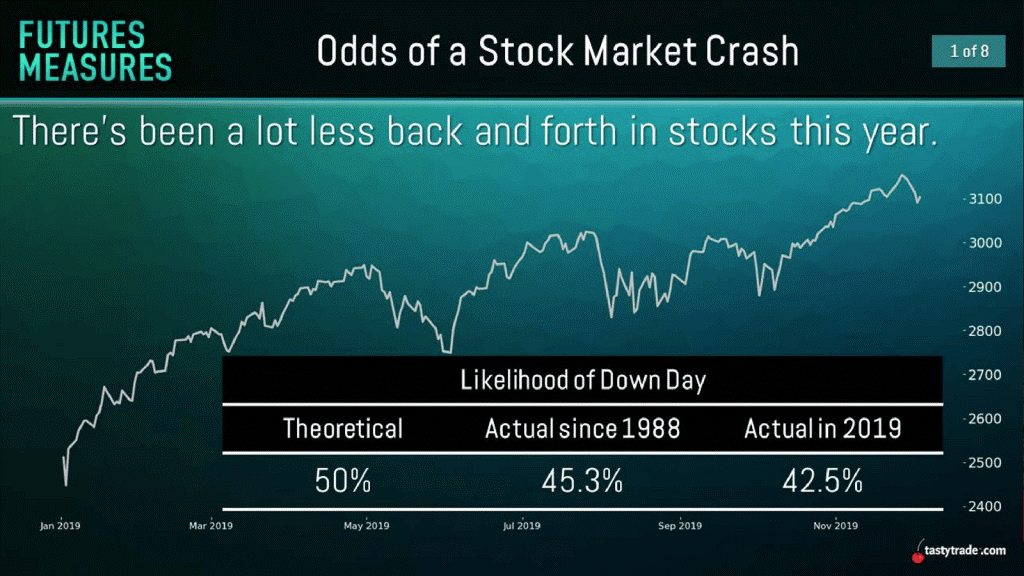
Embora a resposta a essa pergunta seja altamente subjetiva, como se pode ver no gráfico abaixo, 2019 como um todo viu o risco de um dia de baixa no S&P 500 cair abaixo da média histórica:
De acordo com os dados acima, a chance teórica de um dia de “alta” ou “baixa” no S&P 500 é normalmente de 50%. Essa é a mesma probabilidade teórica associada ao lançamento de uma moeda - uma chance de 50% de resultar em uma "cara" ou "coroa".
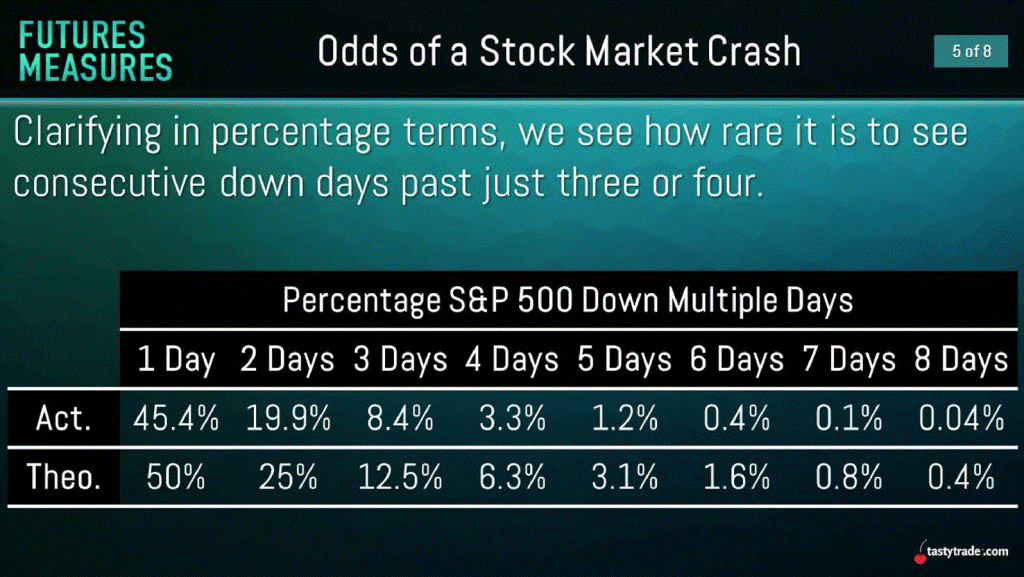
Como mostrado acima, ao comparar os últimos 30 anos de dados históricos no S&P 500 (8.000 dias úteis) a 2019, a chance real de um dia de inatividade durante a negociação de 2019 caiu abaixo da média de 30 anos. Aprofundando-se nos 8.000 dias de negociação dos dados, a equipe de pesquisa verificou várias outras importantes conclusões. Em vez de analisar apenas as chances de um único dia "de baixa", a equipe de pesquisa da tastytrade analisou as chances de dias de baixaconsecutivos. Os gráficos abaixo destacam a probabilidade teórica para números variáveis de dias consecutivos de baixa no S&P 500, bem como o número real observado. Esses dados são expressos em termos percentuais, bem como o número de registros: 
Pelos gráficos acima, pode-se ver que o percentual real de dias de baixa consecutivos no S&P 500 nos últimos 30 anos foi consistentemente menor do que a projeção teórica.
Surpreendentemente, houve apenas três exemplos nos últimos 8.000 dias de negociação nas quais o S&P 500 sofreu oito dias consecutivos de queda. Além disso, a projeção teórica pedia 31 exemplos, em média. Como destacado anteriormente, também houve apenas quatro dias de negociação durante o mesmo período em que o Dow Jones caiu mais de 7% em uma única sessão. Juntando tudo isso, os dados históricos parecem indicar que não há uma alta probabilidade de o mercado de ações dos EUA travar em 2020, especialmente não em uma única sessão. Por outro lado, se o Dow Jones se mover mais de 7% em uma única sessão durante a campanha de 2020, os traders podem querer prestar atenção. Para um índice de ações, um movimento de +7% é efetivamente um evento binário. Desde o início do Dow Jones em 1896, houve 19 casos no total em que o índice caiu mais de 7% em uma única sessão. Quatro desses 19 casos foram observados nas últimas duas décadas, em meio a correções calamitosas e prolongadas.
Traduzido por: Leandro Guerra
Fonte: Binary Events and the Odds of a 2020 Market Correction
Atendendo aos pedidos, trago uma aula específica com um resumo para leigos, curiosos e interessados sobre Álgebra Linear, apresentando as principais propriedades e operações com vetores e matrizes.
|
Archives
December 2020
Categories
All
|
||
RSS Feed
Outspoken Market - Copyright © 2016
